DES¶
基本介绍¶
Data Encryption Standard(DES),数据加密标准,是典型的块加密,其基本信息如下
- 输入 64 位。
- 输出 64 位。
- 密钥 64 位,使用 64 位密钥中的 56 位,剩余的 8 位要么丢弃,要么作为奇偶校验位。
- Feistel 迭代结构
- 明文经过 16 轮迭代得到密文。
- 密文经过类似的 16 轮迭代得到明文。
基本流程¶
给出一张简单的 DES 流程图 。

加密¶
我们可以考虑一下每一轮的加密过程
L_{i+1}=R_i
R_{i+1}=L_i\oplus F(R_i,K_i)
那么在最后的 Permutation 之前,对应的密文为(R_{n+1},L_{n+1})。
解密¶
那么解密如何解密呢?首先我们可以把密文先进行逆置换,那么就可以得到最后一轮的输出。我们这时考虑每一轮
R_i=L_{i+1}
L_i=R_{i+1}\oplus F(L_{i+1},K_i)
因此,(L_0,R_0) 就是加密时第一次置换后的明文。我们只需要再执行逆置换就可以获得明文了。
可以看出,DES 加解密使用同一套逻辑,只是密钥使用的顺序不一致。
核心部件¶
DES 中的核心部件主要包括(这里只给出加密过程的)
- 初始置换
- F 函数
- E 扩展函数
- S 盒,设计标准未给出。
- P 置换
- 最后置换
其中 F 函数如下
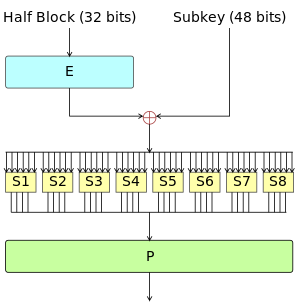
如果对 DES 更加感兴趣,可以进行更加仔细地研究。欢迎提供 PR。
衍生¶
在 DES 的基础上,衍生了以下两种加密方式
- 双重 DES
- 三种 DES
双重 DES¶
双重 DES 使用两个密钥,长度为 112 比特。加密方式如下
C=E_{k2}(E_{k1}(P))
但是双重 DES 不能抵抗中间相遇攻击,我们可以构造如下两个集合
I={E_{k1}(P)}
J=D_{k2}(C)
即分别枚举 K1 和 K2 分别对 P 进行加密和对 C 进行解密。
在我们对 P 进行加密完毕后,可以对加密结果进行排序,这样的复杂度为2^nlog(2^n)=O(n2^n)
当我们对 C 进行解密时,可以每解密一个,就去对应的表中查询。
总的复杂度为还是O(n2^n)。
三重 DES¶
三重 DES 的加解密方式如下
C=E_{k3}(D_{k2}(E_{k1}(P)))
P=D_{k1}(E_{k2}(D_{k3}(C)))
在选择密钥时,可以有两种方法
- 3 个不同的密钥,k1,k2,k3 互相独立,一共 168 比特。
- 2 个不同的密钥,k1 与 k2 独立,k3=k1,112 比特。
攻击方法¶
- 差分攻击
- 线性攻击
2018 N1CTF N1ES¶
基本代码如下
# -*- coding: utf-8 -*-
def round_add(a, b):
f = lambda x, y: x + y - 2 * (x & y)
res = ''
for i in range(len(a)):
res += chr(f(ord(a[i]), ord(b[i])))
return res
def permutate(table, block):
return list(map(lambda x: block[x], table))
def string_to_bits(data):
data = [ord(c) for c in data]
l = len(data) * 8
result = [0] * l
pos = 0
for ch in data:
for i in range(0,8):
result[(pos<<3)+i] = (ch>>i) & 1
pos += 1
return result
s_box = [54, 132, 138, 83, 16, 73, 187, 84, 146, 30, 95, 21, 148, 63, 65, 189, 188, 151, 72, 161, 116, 63, 161, 91, 37, 24, 126, 107, 87, 30, 117, 185, 98, 90, 0, 42, 140, 70, 86, 0, 42, 150, 54, 22, 144, 153, 36, 90, 149, 54, 156, 8, 59, 40, 110, 56,1, 84, 103, 22, 65, 17, 190, 41, 99, 151, 119, 124, 68, 17, 166, 125, 95, 65, 105, 133, 49, 19, 138, 29, 110, 7, 81, 134, 70, 87, 180, 78, 175, 108, 26, 121, 74, 29, 68, 162, 142, 177, 143, 86, 129, 101, 117, 41, 57, 34, 177, 103, 61, 135, 191, 74, 69, 147, 90, 49, 135, 124, 106, 19, 8
9, 38, 21, 41, 17, 155, 83, 38, 159, 179, 19, 157, 68, 105, 151, 166, 171, 122, 179, 114, 52, 183, 89, 107, 113, 65, 161, 141, 18, 121, 95, 4, 95, 101, 81, 156,
17, 190, 38, 84, 9, 171, 180, 59, 45, 15, 34, 89, 75, 164, 190, 140, 6, 41, 188, 77, 165, 105, 5, 107, 31, 183, 107, 141, 66, 63, 10, 9, 125, 50, 2, 153, 156, 162, 186, 76, 158, 153, 117, 9, 77, 156, 11, 145, 12, 169, 52, 57, 161, 7, 158, 110, 191, 43, 82, 186, 49, 102, 166, 31, 41, 5, 189, 27]
def generate(o):
k = permutate(s_box,o)
b = []
for i in range(0, len(k), 7):
b.append(k[i:i+7] + [1])
c = []
for i in range(32):
pos = 0
x = 0
for j in b[i]:
x += (j<<pos)
pos += 1
c.append((0x10001**x) % (0x7f))
return c
class N1ES:
def __init__(self, key):
if (len(key) != 24 or isinstance(key, bytes) == False ):
raise Exception("key must be 24 bytes long")
self.key = key
self.gen_subkey()
def gen_subkey(self):
o = string_to_bits(self.key)
k = []
for i in range(8):
o = generate(o)
k.extend(o)
o = string_to_bits([chr(c) for c in o[0:24]])
self.Kn = []
for i in range(32):
self.Kn.append(map(chr, k[i * 8: i * 8 + 8]))
return
def encrypt(self, plaintext):
if (len(plaintext) % 16 != 0 or isinstance(plaintext, bytes) == False):
raise Exception("plaintext must be a multiple of 16 in length")
res = ''
for i in range(len(plaintext) / 16):
block = plaintext[i * 16:(i + 1) * 16]
L = block[:8]
R = block[8:]
for round_cnt in range(32):
L, R = R, (round_add(L, self.Kn[round_cnt]))
L, R = R, L
res += L + R
return res
显然,我们可以将其视为一个 Feistel 加密的方式,解密函数如下
def decrypt(self,ciphertext):
res = ''
for i in range(len(ciphertext) / 16):
block = ciphertext[i * 16:(i + 1) * 16]
L = block[:8]
R = block[8:]
for round_cnt in range(32):
L, R =R, (round_add(L, self.Kn[31-round_cnt]))
L,R=R,L
res += L + R
return res
最后结果为
➜ baby_N1ES cat challenge.py
from N1ES import N1ES
import base64
key = "wxy191iss00000000000cute"
n1es = N1ES(key)
flag = "N1CTF{*****************************************}"
cipher = n1es.encrypt(flag)
#print base64.b64encode(cipher) # HRlgC2ReHW1/WRk2DikfNBo1dl1XZBJrRR9qECMNOjNHDktBJSxcI1hZIz07YjVx
cipher = 'HRlgC2ReHW1/WRk2DikfNBo1dl1XZBJrRR9qECMNOjNHDktBJSxcI1hZIz07YjVx'
cipher = base64.b64decode(cipher)
print n1es.decrypt(cipher)
➜ baby_N1ES python challenge.py
N1CTF{F3istel_n3tw0rk_c4n_b3_ea5i1y_s0lv3d_/--/}
2019 CISCN part_des¶
题目只给了一个文件:
Round n part_encode-> 0x92d915250119e12b
Key map -> 0xe0be661032d5f0b676f82095e4d67623628fe6d376363183aed373a60167af537b46abc2af53d97485591f5bd94b944a3f49d94897ea1f699d1cdc291f2d9d4a5c705f2cad89e938dbacaca15e10d8aeaed90236f0be2e954a8cf0bea6112e84
考虑到题目名以及数据特征,Round n part_encode 为执行n轮des的中间结果,Key map 应为des的子密钥,要还原出明文只需进行n轮des加密的逆过程即可,解密时注意以下三点。
- 子密钥的选取,对于只进行了n轮的加密结果,解密时应依次使用密钥 n, n-1..., 1。
- des 最后一轮后的操作,未完成的 des 没有交换左右两部分和逆初始置换,因此解密时我们应先对密文进行这两步操作。
- n 的选择,在本题中,我们并不知道 n,但这无关紧要,我们可以尝试所有可能的取值(0-15)flag应为ascii字符串。
解题代码
kkk = 16
def bit_rot_left(lst, pos):
return lst[pos:] + lst[:pos]
class DES:
IP = [
58,50,42,34,26,18,10,2,60,52,44,36,28,20,12,4,
62,54,46,38,30,22,14,6,64,56,48,40,32,24,16,8,
57,49,41,33,25,17,9,1,59,51,43,35,27,19,11,3,
61,53,45,37,29,21,13,5,63,55,47,39,31,23,15,7
]
IP_re = [
40,8,48,16,56,24,64,32,39,7,47,15,55,23,63,31,
38,6,46,14,54,22,62,30,37,5,45,13,53,21,61,29,
36,4,44,12,52,20,60,28,35,3,43,11,51,19,59,27,
34,2,42,10,50,18,58,26,33,1,41,9,49,17,57,25
]
Pbox = [
16,7,20,21,29,12,28,17,1,15,23,26,5,18,31,10,
2,8,24,14,32,27,3,9,19,13,30,6,22,11,4,25
]
E = [
32,1,2,3,4,5,4,5,6,7,8,9,
8,9,10,11,12,13,12,13,14,15,16,17,
16,17,18,19,20,21,20,21,22,23,24,25,
24,25,26,27,28,29,28,29,30,31,32,1
]
PC1 = [
57,49,41,33,25,17,9,1,58,50,42,34,26,18,
10,2,59,51,43,35,27,19,11,3,60,52,44,36,
63,55,47,39,31,23,15,7,62,54,46,38,30,22,
14,6,61,53,45,37,29,21,13,5,28,20,12,4
]
PC2 = [
14,17,11,24,1,5,3,28,15,6,21,10,
23,19,12,4,26,8,16,7,27,20,13,2,
41,52,31,37,47,55,30,40,51,45,33,48,
44,49,39,56,34,53,46,42,50,36,29,32
]
Sbox = [
[
[14,4,13,1,2,15,11,8,3,10,6,12,5,9,0,7],
[0,15,7,4,14,2,13,1,10,6,12,11,9,5,3,8],
[4,1,14,8,13,6,2,11,15,12,9,7,3,10,5,0],
[15,12,8,2,4,9,1,7,5,11,3,14,10,0,6,13],
],
[
[15,1,8,14,6,11,3,4,9,7,2,13,12,0,5,10],
[3,13,4,7,15,2,8,14,12,0,1,10,6,9,11,5],
[0,14,7,11,10,4,13,1,5,8,12,6,9,3,2,15],
[13,8,10,1,3,15,4,2,11,6,7,12,0,5,14,9],
],
[
[10,0,9,14,6,3,15,5,1,13,12,7,11,4,2,8],
[13,7,0,9,3,4,6,10,2,8,5,14,12,11,15,1],
[13,6,4,9,8,15,3,0,11,1,2,12,5,10,14,7],
[1,10,13,0,6,9,8,7,4,15,14,3,11,5,2,12],
],
[
[7,13,14,3,0,6,9,10,1,2,8,5,11,12,4,15],
[13,8,11,5,6,15,0,3,4,7,2,12,1,10,14,9],
[10,6,9,0,12,11,7,13,15,1,3,14,5,2,8,4],
[3,15,0,6,10,1,13,8,9,4,5,11,12,7,2,14],
],
[
[2,12,4,1,7,10,11,6,8,5,3,15,13,0,14,9],
[14,11,2,12,4,7,13,1,5,0,15,10,3,9,8,6],
[4,2,1,11,10,13,7,8,15,9,12,5,6,3,0,14],
[11,8,12,7,1,14,2,13,6,15,0,9,10,4,5,3],
],
[
[12,1,10,15,9,2,6,8,0,13,3,4,14,7,5,11],
[10,15,4,2,7,12,9,5,6,1,13,14,0,11,3,8],
[9,14,15,5,2,8,12,3,7,0,4,10,1,13,11,6],
[4,3,2,12,9,5,15,10,11,14,1,7,6,0,8,13],
],
[
[4,11,2,14,15,0,8,13,3,12,9,7,5,10,6,1],
[13,0,11,7,4,9,1,10,14,3,5,12,2,15,8,6],
[1,4,11,13,12,3,7,14,10,15,6,8,0,5,9,2],
[6,11,13,8,1,4,10,7,9,5,0,15,14,2,3,12],
],
[
[13,2,8,4,6,15,11,1,10,9,3,14,5,0,12,7],
[1,15,13,8,10,3,7,4,12,5,6,11,0,14,9,2],
[7,11,4,1,9,12,14,2,0,6,10,13,15,3,5,8],
[2,1,14,7,4,10,8,13,15,12,9,0,3,5,6,11],
]
]
rout = [1,1,2,2,2,2,2,2,1,2,2,2,2,2,2,1]
def __init__(self):
self.subkey = [[[1, 1, 1, 0, 0, 0, 0, 0, 1, 0, 1, 1, 1, 1, 1, 0, 0, 1, 1, 0, 0, 1, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 0, 1, 0, 1, 0, 1], [1, 1, 1, 1, 0, 0, 0, 0, 1, 0, 1, 1, 0, 1, 1, 0, 0, 1, 1, 1, 0, 1, 1, 0, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 1, 0, 1], [1, 1, 1, 0, 0, 1, 0, 0, 1, 1, 0, 1, 0, 1, 1, 0, 0, 1, 1, 1, 0, 1, 1, 0, 0, 0, 1, 0, 0, 0, 1, 1, 0, 1, 1, 0, 0, 0, 1, 0, 1, 0, 0, 0, 1, 1, 1, 1], [1, 1, 1, 0, 0, 1, 1, 0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 1, 1, 1, 0, 1, 1, 0, 0, 0, 1, 1, 0, 1, 1, 0, 0, 0, 1, 1, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 1, 1], [1, 0, 1, 0, 1, 1, 1, 0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 1, 1, 1, 0, 0, 1, 1, 1, 0, 1, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1, 1, 0, 0, 1, 1, 1], [1, 0, 1, 0, 1, 1, 1, 1, 0, 1, 0, 1, 0, 0, 1, 1, 0, 1, 1, 1, 1, 0, 1, 1, 0, 1, 0, 0, 0, 1, 1, 0, 1, 0, 1, 0, 1, 0, 1, 1, 1, 1, 0, 0, 0, 0, 1, 0], [1, 0, 1, 0, 1, 1, 1, 1, 0, 1, 0, 1, 0, 0, 1, 1, 1, 1, 0, 1, 1, 0, 0, 1, 0, 1, 1, 1, 0, 1, 0, 0, 1, 0, 0, 0, 0, 1, 0, 1, 0, 1, 0, 1, 1, 0, 0, 1], [0, 0, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 0, 1, 1, 1, 1, 0, 1, 1, 0, 0, 1, 0, 1, 0, 0, 1, 0, 1, 1, 1, 0, 0, 1, 0, 1, 0, 0, 0, 1, 0, 0, 1, 0, 1, 0], [0, 0, 1, 1, 1, 1, 1, 1, 0, 1, 0, 0, 1, 0, 0, 1, 1, 1, 0, 1, 1, 0, 0, 1, 0, 1, 0, 0, 1, 0, 0, 0, 1, 0, 0, 1, 0, 1, 1, 1, 1, 1, 1, 0, 1, 0, 1, 0], [0, 0, 0, 1, 1, 1, 1, 1, 0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 0, 1, 1, 1, 0, 1, 0, 0, 0, 1, 1, 1, 0, 0, 1, 1, 0, 1, 1, 1, 0, 0, 0, 0, 1, 0, 1, 0, 0, 1], [0, 0, 0, 1, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 0, 1, 1, 0, 0, 1, 1, 1, 0, 1, 0, 1, 0, 0, 1, 0, 1, 0, 0, 1, 0, 1, 1, 1, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0], [0, 1, 0, 1, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 0, 0, 1, 0, 1, 0, 1, 1, 0, 1, 1, 0, 0, 0, 1, 0, 0, 1, 1, 1, 1, 0, 1, 0, 0, 1, 0, 0, 1, 1, 1, 0, 0, 0], [1, 1, 0, 1, 1, 0, 1, 1, 1, 0, 1, 0, 1, 1, 0, 0, 1, 0, 1, 0, 1, 1, 0, 0, 1, 0, 1, 0, 0, 0, 0, 1, 0, 1, 0, 1, 1, 1, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0], [1, 1, 0, 1, 1, 0, 0, 0, 1, 0, 1, 0, 1, 1, 1, 0, 1, 0, 1, 0, 1, 1, 1, 0, 1, 1, 0, 1, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 1, 0, 1, 1, 0], [1, 1, 1, 1, 0, 0, 0, 0, 1, 0, 1, 1, 1, 1, 1, 0, 0, 0, 1, 0, 1, 1, 1, 0, 1, 0, 0, 1, 0, 1, 0, 1, 0, 1, 0, 0, 1, 0, 1, 0, 1, 0, 0, 0, 1, 1, 0, 0], [1, 1, 1, 1, 0, 0, 0, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 0, 0, 1, 1, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 1, 0, 1, 1, 1, 0, 1, 0, 0, 0, 0, 1, 0, 0]], [[1, 1, 1, 1, 0, 0, 0, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 0, 0, 1, 1, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 1, 0, 1, 1, 1, 0, 1, 0, 0, 0, 0, 1, 0, 0], [1, 1, 1, 1, 0, 0, 0, 0, 1, 0, 1, 1, 1, 1, 1, 0, 0, 0, 1, 0, 1, 1, 1, 0, 1, 0, 0, 1, 0, 1, 0, 1, 0, 1, 0, 0, 1, 0, 1, 0, 1, 0, 0, 0, 1, 1, 0, 0], [1, 1, 0, 1, 1, 0, 0, 0, 1, 0, 1, 0, 1, 1, 1, 0, 1, 0, 1, 0, 1, 1, 1, 0, 1, 1, 0, 1, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 1, 0, 1, 1, 0], [1, 1, 0, 1, 1, 0, 1, 1, 1, 0, 1, 0, 1, 1, 0, 0, 1, 0, 1, 0, 1, 1, 0, 0, 1, 0, 1, 0, 0, 0, 0, 1, 0, 1, 0, 1, 1, 1, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0], [0, 1, 0, 1, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 0, 0, 1, 0, 1, 0, 1, 1, 0, 1, 1, 0, 0, 0, 1, 0, 0, 1, 1, 1, 1, 0, 1, 0, 0, 1, 0, 0, 1, 1, 1, 0, 0, 0], [0, 0, 0, 1, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 0, 1, 1, 0, 0, 1, 1, 1, 0, 1, 0, 1, 0, 0, 1, 0, 1, 0, 0, 1, 0, 1, 1, 1, 0, 0, 0, 1, 1, 1, 0, 0, 0, 0], [0, 0, 0, 1, 1, 1, 1, 1, 0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 0, 1, 1, 1, 0, 1, 0, 0, 0, 1, 1, 1, 0, 0, 1, 1, 0, 1, 1, 1, 0, 0, 0, 0, 1, 0, 1, 0, 0, 1], [0, 0, 1, 1, 1, 1, 1, 1, 0, 1, 0, 0, 1, 0, 0, 1, 1, 1, 0, 1, 1, 0, 0, 1, 0, 1, 0, 0, 1, 0, 0, 0, 1, 0, 0, 1, 0, 1, 1, 1, 1, 1, 1, 0, 1, 0, 1, 0], [0, 0, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 0, 1, 1, 1, 1, 0, 1, 1, 0, 0, 1, 0, 1, 0, 0, 1, 0, 1, 1, 1, 0, 0, 1, 0, 1, 0, 0, 0, 1, 0, 0, 1, 0, 1, 0], [1, 0, 1, 0, 1, 1, 1, 1, 0, 1, 0, 1, 0, 0, 1, 1, 1, 1, 0, 1, 1, 0, 0, 1, 0, 1, 1, 1, 0, 1, 0, 0, 1, 0, 0, 0, 0, 1, 0, 1, 0, 1, 0, 1, 1, 0, 0, 1], [1, 0, 1, 0, 1, 1, 1, 1, 0, 1, 0, 1, 0, 0, 1, 1, 0, 1, 1, 1, 1, 0, 1, 1, 0, 1, 0, 0, 0, 1, 1, 0, 1, 0, 1, 0, 1, 0, 1, 1, 1, 1, 0, 0, 0, 0, 1, 0], [1, 0, 1, 0, 1, 1, 1, 0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 1, 1, 1, 0, 0, 1, 1, 1, 0, 1, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1, 1, 0, 0, 1, 1, 1], [1, 1, 1, 0, 0, 1, 1, 0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 1, 1, 1, 0, 1, 1, 0, 0, 0, 1, 1, 0, 1, 1, 0, 0, 0, 1, 1, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 1, 1], [1, 1, 1, 0, 0, 1, 0, 0, 1, 1, 0, 1, 0, 1, 1, 0, 0, 1, 1, 1, 0, 1, 1, 0, 0, 0, 1, 0, 0, 0, 1, 1, 0, 1, 1, 0, 0, 0, 1, 0, 1, 0, 0, 0, 1, 1, 1, 1], [1, 1, 1, 1, 0, 0, 0, 0, 1, 0, 1, 1, 0, 1, 1, 0, 0, 1, 1, 1, 0, 1, 1, 0, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 1, 0, 1], [1, 1, 1, 0, 0, 0, 0, 0, 1, 0, 1, 1, 1, 1, 1, 0, 0, 1, 1, 0, 0, 1, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 0, 1, 0, 1, 0, 1]]]
def permute(self, lst, tb):
return [lst[i-1] for i in tb]
def f(self,riti,subkeyi):
tmp = [i^j for i,j in zip(subkeyi,self.permute(riti,DES.E))]
return self.permute(sum([[int(l) for l in str(bin(DES.Sbox[i][int(str(tmp[6*i])+str(tmp[6*i+5]),2)][int("".join(str(j) for j in tmp[6*i+1:6*i+5]),2)])[2:].zfill(4))] for i in range(8)],[]),DES.Pbox)
def des_main(self,m,mark):
sbkey = self.subkey[0]
#if mark == 'e' else self.subkey[1]
# tmp = self.permute([int(i) for i in list((m).ljust(64,"0"))],self.IP)
tmp = [int(i) for i in list((m).ljust(64,"0"))]
global kkk
print(kkk)
for i in range(kkk):
tmp = tmp[32:] + [j^k for j,k in zip(tmp[:32],self.f(tmp[32:],sbkey[i if mark != 'd' else kkk-1-i]))]
return "".join([str(i) for i in self.permute(tmp[32:]+tmp[:32],self.IP_re)])
def des_encipher(self,m):
m = "".join([bin(ord(i))[2:].zfill(8) for i in m])
des_en = self.des_main(m,'e')
return "".join([chr(int(des_en[i*8:i*8+8],2)) for i in range(8)])
def des_decipher(self,c):
c = "".join([bin(ord(i))[2:].zfill(8) for i in c])
des_de = self.des_main(c,'d')
return "".join([chr(int(des_de[i*8:i*8+8],2)) for i in range(8)])
def test():
import base64
global kkk
while kkk >=0:
desobj = DES()
# cipher = desobj.des_encipher("12345678")
cipher = '\x01\x19\xe1+\x92\xd9\x15%'
message1 = desobj.des_decipher(cipher)
print(message1)
kkk -= 1
if __name__=='__main__':
test()
解密结果(部分):
14
t-ÏEÏx§
13
y0ur9Ood
12
µp^Ûé=¹
11
)Á`rûÕû
可以看出n为13,flag为flag{y0ur9Ood}
参考¶
- 清华大学研究生数据安全课程课件
- https://en.wikipedia.org/wiki/Data_Encryption_Standard