CVP¶
CVP是Lattice-based cryptography中尤为重要的一个问题。
问题的基本定义如下:给定格L的一组基与向量\mathbf{v},找到在L上离\mathbf{v}最近的一个向量。
Algorithms¶
Babai's nearest plane algorithm¶
该算法输入一组格L(秩为n)的基B和一个目标向量\mathbf{t},输出CVP问题的近似解。
- 近似因子为\gamma = 2^{\frac{n}{2}}
具体算法:
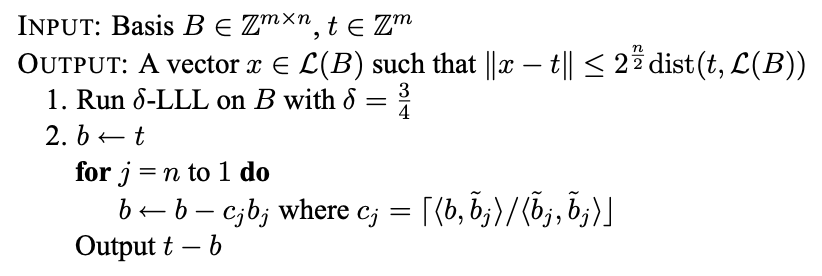
- 其中c_j为Gram-schmidt正交化中的系数取整,也即proj_{b_{j}}(b)的取整。
对于该算法第二步的个人理解:在格基规约和正交化过后的基B中找到一个最靠近\mathbf{t}的线性组合。
Babai’s Rounding Technique¶
该算法是Babai's nearest plane algorithm的一个变种。
步骤可以表示为:
N = rank(B), w = target
- B' = LLL(B)
- Find a linear combination [l_0, ... l_N] such that w = sum(l_i * b'_i).
* (b'_i is the i-th vector in the LLL-reduced basis B')
- Round each l_i to it's closest integer l'_i.
- Result v = sum(l'_i * b'_i)
相关内容¶
Hidden number problem¶
HNP的定义如下:
给定质数p、许多t \in \mathbb{F}_p以及每一个对应的MSB_{l,p}(\alpha t),找出对应的\alpha。
- MSB_{l,p}(x)表示任一满足 \lvert (x \mod p) - u \rvert \le \frac{p}{2^{l+1}} 的整数 u,近似为取x \mod p的l个最高有效位。
根据参考3中的描述,当l \approx \log^{\frac{1}{2}}{p}时,有如下算法可以解决HNP:
我们可以将此问题转化为一个由该矩阵生成的格上的CVP问题:
\left[ \begin{matrix} p & 0 & \dots & 0 & 0 \\ 0 & p & \ddots & \vdots & \vdots \\ \vdots & \ddots & \ddots & 0 & \vdots \\ 0 & 0 & \dots & p & 0 \\ t_1 & t_2 & \dots & t_{n} & \frac{1}{2^{l+1}} \end{matrix} \right]
我们需要找到在格上离\mathbf{u}=(u_1, u_2, \dots, u_{n}, 0)最近的向量,所以在这里,我们可以采用Babai's nearest plane algorithm。最终我们可以得到一组向量 \mathbf{v}=(\alpha \cdot t_1 \mod p, \alpha \cdot t_2 \mod p, \dots, \frac{\alpha}{2^{l+1}}),从而算出 \alpha。
BCTF 2018 - guess_number¶
题目提供了服务器端的代码:
import random, sys
from flag import FLAG
import gmpy2
def msb(k, x, p):
delta = p >> (k + 1)
ui = random.randint(x - delta, x + delta)
return ui
def main():
p = gmpy2.next_prime(2**160)
for _ in range(5):
alpha = random.randint(1, p - 1)
# print(alpha)
t = []
u = []
k = 10
for i in range(22):
t.append(random.randint(1, p - 1))
u.append(msb(k, alpha * t[i] % p, p))
print(str(t))
print(str(u))
guess = raw_input('Input your guess number: ')
guess = int(guess)
if guess != alpha:
exit(0)
if __name__ == "__main__":
main()
print(FLAG)
可以看到,程序一共执行5轮。在每一轮,程序会生成一个随机的\alpha和22个随机的t_i。对于每一个t_i,程序会取u_i = MSB_{10,p}(\alpha\cdot{t_i\mod{p}}),随后发送给客户端。我们需要根据提供的t_i和u_i计算出对应的\alpha。可以看到,该问题是一个典型的Hidden number problem,于是可以使用上述算法解决:
import socket
import ast
import telnetlib
#HOST, PORT = 'localhost', 9999
HOST, PORT = '60.205.223.220', 9999
s = socket.socket()
s.connect((HOST, PORT))
f = s.makefile('rw', 0)
def recv_until(f, delim='\n'):
buf = ''
while not buf.endswith(delim):
buf += f.read(1)
return buf
p = 1461501637330902918203684832716283019655932542983
k = 10
def solve_hnp(t, u):
# http://www.isg.rhul.ac.uk/~sdg/igor-slides.pdf
M = Matrix(RationalField(), 23, 23)
for i in xrange(22):
M[i, i] = p
M[22, i] = t[i]
M[22, 22] = 1 / (2 ** (k + 1))
def babai(A, w):
A = A.LLL(delta=0.75)
G = A.gram_schmidt()[0]
t = w
for i in reversed(range(A.nrows())):
c = ((t * G[i]) / (G[i] * G[i])).round()
t -= A[i] * c
return w - t
closest = babai(M, vector(u + [0]))
return (closest[-1] * (2 ** (k + 1))) % p
for i in xrange(5):
t = ast.literal_eval(f.readline().strip())
u = ast.literal_eval(f.readline().strip())
alpha = solve_hnp(t, u)
recv_until(f, 'number: ')
s.send(str(alpha) + '\n')
t = telnetlib.Telnet()
t.sock = s
t.interact()