离散对数¶
基本定义¶
在了解离散对数时,我们先来了解几个基本定义。
定义1
在群 G 中,g 为 G 的生成元,也就是说群 G 中每一个元素都可以写成 y=g^k,我们称 k 为 y 在群 G 中的对数。
定义2
设 m\geq 1,(a,m)=1 ,使得 a^d \equiv 1\pmod m 成立的最小正整数 d 称为 a 对模 m 的指数或者阶,我们一般将其记为 \delta_m(a)。
定义3
当 \delta_m(a)=\varphi(m) 时,称 a 是模 m 的原根,简称 m 的原根。
一些性质¶
性质1
使得 a^d \equiv 1\pmod m 成立的最小正整数 d ,必有d\mid\varphi(m)。
性质2
模 m 剩余系存在原根的充要条件是 m=2,4,p^{\alpha},2p^{\alpha} ,其中 p 为奇素数, \alpha 为正整数。
离散对数问题¶
已知 g,p,y ,对于方程 y\equiv g^x \pmod p ,求解 x 是一个难解问题。但是当 p 具有一定的特性时就可能可以求解,比如,这个群的阶是一个光滑数。
正是上述这个问题构成了目前很大一部分现代密码学,包括 Diffie–Hellman 密钥交换, ElGamal 算法,ECC 等。
离散对数求解方式¶
暴力破解¶
给定 y\equiv g^x \pmod p,我们可以暴力枚举 x 从而得到真正的 x 的值。
Baby-step giant-step¶
这一方法通常被称为小步大步法,这一方法使用了中间相遇攻击的思想。
我们可以令 x=im+j,其中 m= \lceil \sqrt n\rceil ,那么整数 i 和 j 都在 0 到 m 的范围内。
因此
也就是
那么我们就可以枚举所有的 j 并进行计算,并将其存储到一个集合 S 中,然后我们再次枚举 i,计算 y(g^{-m})^i,一旦我们发现计算的结果在集合 S 中,则说明我们得到了一个碰撞,进而得到了 i 和 j。
这显然是一个时间与空间的折中的方式,我们将一个 O(n) 的时间复杂度,O(1) 空间复杂度的算法转换为了一个O(\sqrt n)的时间复杂度和O(\sqrt n) 的空间复杂度的算法。
其中
- 每一次 j 的增加表示“baby-step”,一次乘上 g。
- 每一次 i 的增加表示“giant-step”,一次乘上 g^{-m} 。
def bsgs(g, y, p):
m = int(ceil(sqrt(p - 1)))
S = {pow(g, j, p): j for j in range(m)}
gs = pow(g, p - 1 - m, p)
for i in range(m):
if y in S:
return i * m + S[y]
y = y * gs % p
return None
Pollard’s ρ algorithm¶
我们可以以O(\sqrt n)的时间复杂度和O(1) 的空间复杂度来解决上述问题。具体原理请自行谷歌。
Pollard’s kangaroo algorithm¶
如果我们知道 x 的范围为 a \leq x \leq b,那么我们可以以O(\sqrt{b-a}) 的时间复杂度解决上述问题。具体原理请自行谷歌。
Pohlig-Hellman algorithm¶
不妨假设上述所提到的群关于元素 g 的阶为 n, n 为一个光滑数: n=\prod\limits_{i=1}^r p_i^{e_i}。
- 对于每个 i \in \{1,\ldots,r\} :
- 计算 g_i \equiv g^{n/p_i^{e_i}} \pmod m。根据拉格朗日定理, g_i 在群中的阶为 p_i^{e_i} 。
- 计算 y_i \equiv y^{n/p_i^{e_i}} \equiv g^{xn/p_i^{e_i}} \equiv g_i^{x} \equiv g_i^{x \bmod p_i^{e_i}} \equiv g_i^{x_i} \pmod m,这里我们知道 y_i,m,g_i,而x_i 的范围为[0,p_i^{e_i}),由 n 是一个光滑数,可知其范围较小,因此我们可以使用 Pollard’s kangaroo algorithm 等方法快速求得x_i。
- 根据上述的推导,我们可以得到对于 i \in \{1,\ldots,r\} ,x \equiv x_i \pmod{p_i^{e_i}} ,该式可用中国剩余定理求解。
上述过程可用下图简单描述:
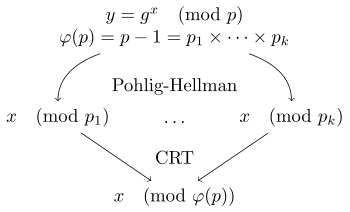
其复杂度为O\left(\sum\limits _i e_i\left(\log n+\sqrt{p_i}\right)\right),可以看出复杂度还是很低的。
但当 n 为素数,m=2n+1,那么复杂度和 O(\sqrt m) 是几乎没有差别的。
2018 国赛 crackme java¶
代码如下
import java.math.BigInteger;
import java.util.Random;
public class Test1 {
static BigInteger two =new BigInteger("2");
static BigInteger p = new BigInteger("11360738295177002998495384057893129964980131806509572927886675899422214174408333932150813939357279703161556767193621832795605708456628733877084015367497711");
static BigInteger h= new BigInteger("7854998893567208831270627233155763658947405610938106998083991389307363085837028364154809577816577515021560985491707606165788274218742692875308216243966916");
/*
Alice write the below algorithm for encryption.
The public key {p, h} is broadcasted to everyone.
@param val: The plaintext to encrypt.
We suppose val only contains lowercase letter {a-z} and numeric charactors, and is at most 256 charactors in length.
*/
public static String pkEnc(String val){
BigInteger[] ret = new BigInteger[2];
BigInteger bVal=new BigInteger(val.toLowerCase(),36);
BigInteger r =new BigInteger(new Random().nextInt()+"");
ret[0]=two.modPow(r,p);
ret[1]=h.modPow(r,p).multiply(bVal);
return ret[0].toString(36)+"=="+ret[1].toString(36);
}
/* Alice write the below algorithm for decryption. x is her private key, which she will never let you know.
public static String skDec(String val,BigInteger x){
if(!val.contains("==")){
return null;
}
else {
BigInteger val0=new BigInteger(val.split("==")[0],36);
BigInteger val1=new BigInteger(val.split("==")[1],36);
BigInteger s=val0.modPow(x,p).modInverse(p);
return val1.multiply(s).mod(p).toString(36);
}
}
*/
public static void main(String[] args) throws Exception {
System.out.println("You intercepted the following message, which is sent from Bob to Alice:");
BigInteger bVal1=new BigInteger("a9hgrei38ez78hl2kkd6nvookaodyidgti7d9mbvctx3jjniezhlxs1b1xz9m0dzcexwiyhi4nhvazhhj8dwb91e7lbbxa4ieco",36);
BigInteger bVal2=new BigInteger("2q17m8ajs7509yl9iy39g4znf08bw3b33vibipaa1xt5b8lcmgmk6i5w4830yd3fdqfbqaf82386z5odwssyo3t93y91xqd5jb0zbgvkb00fcmo53sa8eblgw6vahl80ykxeylpr4bpv32p7flvhdtwl4cxqzc",36);
BigInteger r =new BigInteger(new Random().nextInt()+"");
System.out.println(r);
System.out.println(bVal1);
System.out.println(bVal2);
System.out.println("a9hgrei38ez78hl2kkd6nvookaodyidgti7d9mbvctx3jjniezhlxs1b1xz9m0dzcexwiyhi4nhvazhhj8dwb91e7lbbxa4ieco==2q17m8ajs7509yl9iy39g4znf08bw3b33vibipaa1xt5b8lcmgmk6i5w4830yd3fdqfbqaf82386z5odwssyo3t93y91xqd5jb0zbgvkb00fcmo53sa8eblgw6vahl80ykxeylpr4bpv32p7flvhdtwl4cxqzc");
System.out.println("Please figure out the plaintext!");
}
}
基本功能为计算
r_0=2^r \bmod p
r_1 =b*h^r \bmod p
可以发现,r 的范围为 [0,2^{32}),所以我们可以使用 BSGS 算法,如下
from sage.all import *
c1 = int(
'a9hgrei38ez78hl2kkd6nvookaodyidgti7d9mbvctx3jjniezhlxs1b1xz9m0dzcexwiyhi4nhvazhhj8dwb91e7lbbxa4ieco',
36
)
c2 = int(
'2q17m8ajs7509yl9iy39g4znf08bw3b33vibipaa1xt5b8lcmgmk6i5w4830yd3fdqfbqaf82386z5odwssyo3t93y91xqd5jb0zbgvkb00fcmo53sa8eblgw6vahl80ykxeylpr4bpv32p7flvhdtwl4cxqzc',
36
)
print c1, c2
p = 11360738295177002998495384057893129964980131806509572927886675899422214174408333932150813939357279703161556767193621832795605708456628733877084015367497711
h = 7854998893567208831270627233155763658947405610938106998083991389307363085837028364154809577816577515021560985491707606165788274218742692875308216243966916
# generate the group
const2 = 2
const2 = Mod(const2, p)
c1 = Mod(c1, p)
c2 = Mod(c2, p)
h = Mod(h, p)
print '2', bsgs(const2, c1, bounds=(1, 2 ^ 32))
r = 152351913
num = long(c2 / (h**r))
print num